Abacus is a Latin word that has its origins in the Greek words abax or abakon (meaning "table" or "tablet") which in turn, possibly originated from the Semitic word abq, meaning "sand" 1.
Why does the abacus exist?
It is difficult to imagine counting without numbers, but there was a time when written numbers did not exist. The earliest counting device was the human hand and its fingers. Then, as larger quantities (larger than ten human-fingers could represent) were counted, various natural items like pebbles and twigs were used to help count. Merchants who traded goods not only needed a way to count goods they bought and sold, but also to calculate the cost of those goods. Until numbers were invented, counting devices were used to make everyday calculations.
The difference between a counting board and an abacus
It is important to distinguish the early abacuses (or abaci) known as counting boards from the modern abaci. The counting board is a piece of wood, stone or metal with carved grooves or painted lines between which beads, pebbles or metal discs were moved. The abacus is a device, usually of wood (plastic, in recent times), having a frame that holds rods with freely-sliding beads mounted on them.
Both the abacus and the counting board are mechanical aids used for counting; they are not calculators in the sense we use the word today. The person operating the abacus performs calculations in their head and uses the abacus as a physical aid to keep track of the sums, the carrys, etc.
What did the first counting board look like?
The earliest counting boards are forever lost because of the perishable materials used in their construction. However, educated guesses can be made about their construction, based on early writings of Plutarch (a priest at the Oracle at Delphi) and others.
In outdoor markets of those times, the simplest counting board involved drawing lines in the sand with fingers or a stylus, and placing pebbles between those lines as place-holders representing numbers (the spaces between 2 lines would represent the units 10s, 100s, etc.). The more affluent, could afford small wooden tables having raised borders that were filled with sand (usually coloured blue or green). Another benefit of these counting boards on tables was that they could be moved without disturbing the calculation and they could also be used indoors.
With the need for something more durable and portable, wooden boards with grooves carved into them, were then created and wooden markers (small discs) were used as place-holders. The wooden boards then gave way to even more more permanent materials like marble and metal with stone and metal markers.

The Salamis Tablet: The oldest counting board, made of marble, has a large crack across the middle. Photo from the National Museum of Epigraphy, Athens. (Click to enlarge)
The Salamis Tablet
The oldest surviving counting board is the Salamis tablet (originally thought to be a gaming board), used by the Babylonians circa 300 B.C., discovered in 1846 on the island of Salamis.
It is a slab of white marble measuring 149cm in length, 75cm in width and 4.5cm thick, on which are 5 groups of markings. In the center of the tablet are a set of 5 parallel lines equally divided by a vertical line, capped with a semi-circle at the intersection of the bottom-most horizontal line and the single vertical line. Below these lines is a wide space with a horizontal crack dividing it. Below this crack is another group of eleven parallel lines, again divided into two sections by a line perpendicular to them but with the semi-circle at the top of the intersection; the third, sixth and ninth of these lines are marked with a cross where they intersect with the vertical line. Three sets of Greek symbols (numbers from the acrophonic system) are arranged along the left, right and bottom edges of the tablet2.
Evolution: The Abacus Through the Ages
The evolution of the abacus can be divided into three ages: Ancient Times, Middle Ages, and Modern Times. The time-line below traces the developing abacus from its beginnings circa 500 B.C., to the present.

Evolutionary Time-line: This time-line shows the evolution from the earliest counting board to the present day abacus. (Compared to the rate of progress in last one-thousand years, the progress during the first one-thousand years of civilization was rather slow).
Ancient Times
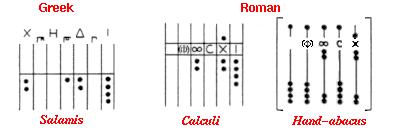
Ancient Times: The Salamis Tablet, the Roman Calculi and Hand-abacus are from the period c. 300 B.C to c. 500 A.D.
During Greek and Roman times, counting boards, like the Roman hand-abacus, that survive are constructed from stone and metal (as a point of reference, the Roman empire fell circa 500 A.D.).
The Middle Ages

Middle Ages: The Apices, the coin-board and the Line-board are from the period c. 5 A.D. to c. 1400 A.D.
Wood was the primary material from which counting boards were manufactured; the orientation of the beads switched from vertical to horizontal. As arithmetic (counting using written numbers) gained popularity in the latter part of the Middle Ages, the use of the abacus began to diminish in Europe.
Modern Times
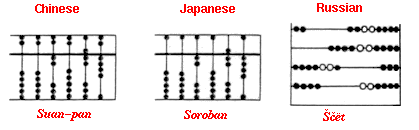
Modern Times: The Suan-pan, the Soroban and the Schoty are from the period c. 1200 A.D to the present.
The abacus as we know it today, appeared circa 1200 A.D. in China; in Chinese, it is called suan-pan. On each rod, this classic Chinese abacus has 2 beads on the upper deck and 5 on the lower deck; such an abacus is also referred to as a 2/5 abacus. The 2/5 style survived unchanged until about 1850 at which time the 1/5 (one bead on the top deck and five beads on the bottom deck) abacus appeared.
Circa 1600 A.D., use and evolution of the Chinese 1/5 abacus was begun by the Japanese via Korea. In Japanese, the abacus is called soroban. The 1/4 abacus, a style preferred and still manufactured in Japan today, appeared circa 1930. The 1/5 models are rare today and 2/5 models are rare outside of China (excepting Chinese communities in North America and elsewhere).
It is thought that early Christians brought the abacus to the East (note that both the suan-pan and the Roman hand-abacus have a vertical orientation).
There have been recent suggestions of a Mesoamerican (the Aztec civilization that existed in present day Mexico) abacus called the Nepohualtzitzin, circa 900-1000 A.D., where the counters were made from kernels of maize threaded through strings mounted on a wooden frame. There is also debate about the Incan Khipu— was it a three-dimensional binary calculator or a form of writing? (q.v. Talking Knots of the Incas).
The schoty, is a Russian abacus invented in the 17th century and still used today in some parts.The Abacus Today
The image on the right is a cover of a manual published in 1958 by Lee Kai-chen, the inventor of this "new" abacus designed with 4 decks (essentially, it consists of 2 stacked abaci; the top abacus is a small 1/4 soroban and the bottom one is a 2/5 suan-pan).
The author claims that multiplication and division are easier using this modified abacus and includes instructions for determining square roots and cubic roots of numbers.

